Calculadoras de Momentos de Inércia

Seções Transversais Mais Comuns em Engenharia

Momento de inércia de uma seção retangular

Momento de inércia de uma seção tubular retangular

Seção Transversal	Calculadora Online
Retangular	Ver calculadora
Tubular Retangular	Ver calculadora
Circular Cheia	Ver calculadora
Circular Vazada	Ver calculadora
Seção em I	Ver calculadora
Seção em C	Ver calculadora
Seção em T	Ver calculadora

O que é o momento de inércia?

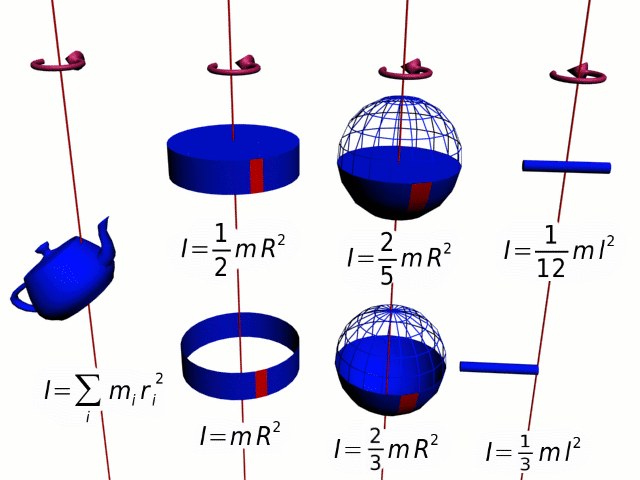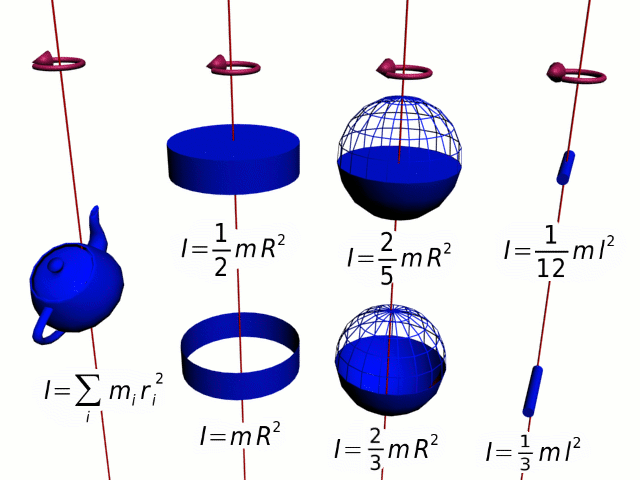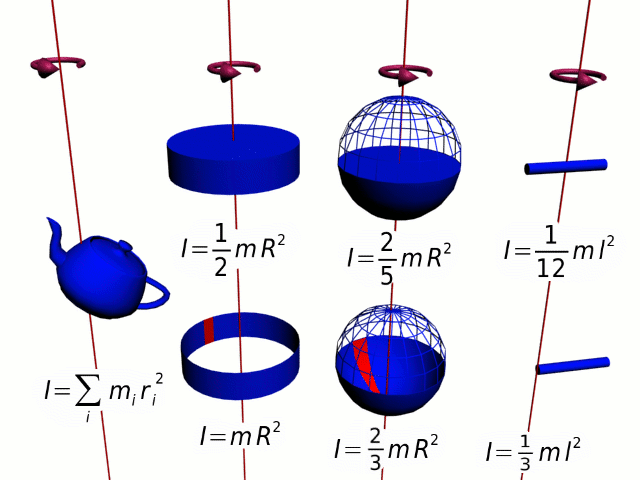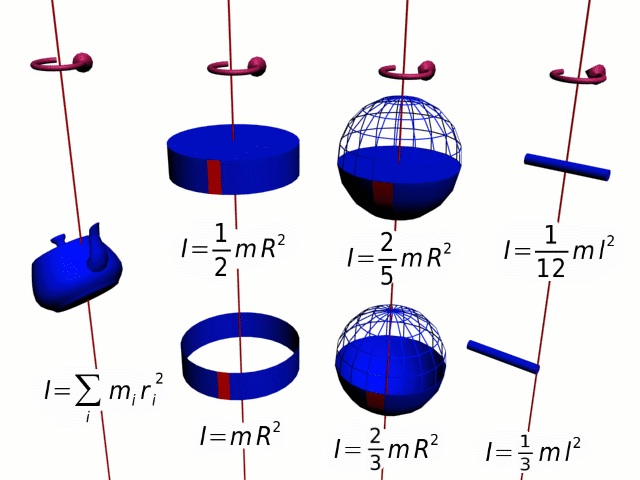
O momento de inércia é uma grandeza física relacionada com a inércia da rotação. O momento de inércia pode ser definido, de uma forma muito resumida, como a resistência de um determinado corpo à mudança da sua velocidade de rotação.

Já os momentos de inércia de área são propriedades geométricas da seção transversal de elementos estruturais. O EngiObra disponibiliza toda a informação de que necessita para fazer o cálculo do momento de inércia da área.

Nesta seção vai encontrar a informação que procura para calcular o momento de inércia de área para diversas seções transversais, incluindo: retangular, tubular retangular, circular cheia, circular vazada, seção em I, seção em C e seção em T.

Antes de avançarmos para as soluções de cálculo do momento de inércia, é importante diferenciar os dois conceitos fundamentais:

Os momentos de inércia ou momentos de inércia de massa são referentes ao momento de inércia de sólidos (3D) enquanto os momentos de inércia de área são referentes aos momentos de inércia de uma seção bidimensional (2D).

Pode agora começar a fazer o cálculo do momento de inércia, utilizando a informação que aqui é apresentada.

Serviço: Projetos de estabilidade engiobra

Momentos de inércia de área

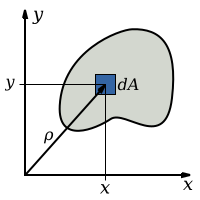
Nestas calculadoras online é possível calcular os momentos de inércia de área e o momento polar de inércia de uma determinada seção transversal.

O momento de inércia ou também conhecido como o segundo momento de inércia é determinado pela seguinte formula geral.

Não ouve necessidade de fazer uma calculadora independente para o momento polar de inercia, uma vez que o Momento Polar de inercia é dado pela seguinte soma:

J = (Ix+Iy)

Em que;

J – Momento polar de inercia
Ix – Momento de inercia segundo x
Iy – Momento de inercia segundo y